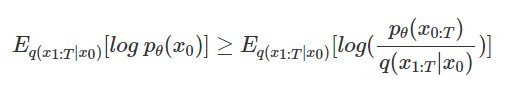今天的內容主要會介紹 diffusion model 學習目標的數學形式，和之前介紹的 VAE 與 flow-based model 一樣，diffusion model 也是基於最大概似估計（maximum likelihood estimation）學習產生與真實資料接近的影像。由於之前對於最大概似估計都簡單帶過，因此在今天文章的一開始，我想先比較詳盡的介紹這個方法，以及它如何和生成任務的學習目標有關～

最大概似估計（Maximum Likelihood Estimation，MLE）

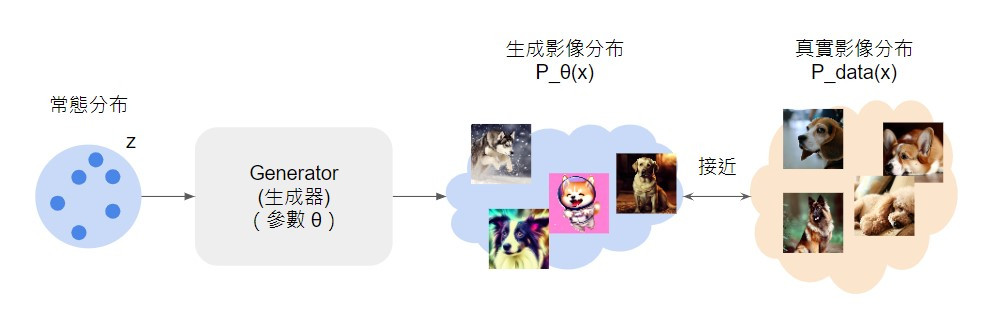
回顧一下影像生成任務的目標，就是希望生成模型能產生一個影像分布，而這個分布和真實影像分布越接近越好，也就如上圖所示。

至於什麼是 likelihood 呢？當我們從真實影像分布 p_data(x) 抽樣一些影像樣本 {x_1, x_2, ..., x_m}，然而計算生成影像分布基於現在的模型參數能產生出這些真實樣本的可能性 p_θ(xi)，就是 likelihood。而 maximum likelihood estimation 就是我們要找到一組模型參數 θ，它能讓生成影像模型產生真實樣本的可能性最大，即能最大化 likelihood 的參數組合，它的數學形式如下：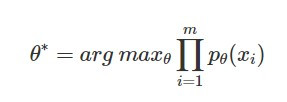

找出讓生成影像分布最有可能產生真實影像的參數，直覺上就已經蠻符合圖像生成任務所要達成的目標了，但實際上我們還可以透過一些推導，就會發現最大化 likelihood 其實就是最小化生成影像分布 p_θ(x) 和真實影像分布 p_data(x) 的 KL divergence（還記得 divergence 可以代表兩個分布的差距嗎～），對這部分有興趣可參考以下的推導：

Diffusion model 的學習目標

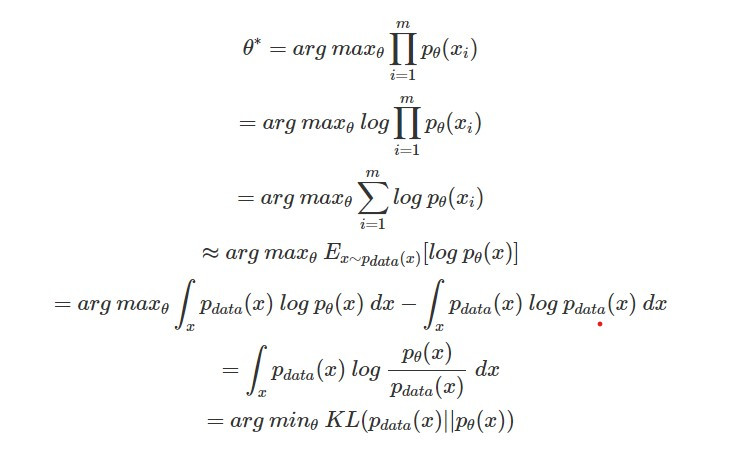
Diffusion model 其實和 VAE 的原理很相像，都是透過 variational inference 去近似原本複雜的分布。

首先我們先來回顧一下 VAE。VAE 其實不是直接找到最大化 likelihood 的生成模型參數組合，它實際上最大化的是 likelihood 的 lower bound。在先前 VAE 的數學原理介紹，我們也已經推導出 lower bound 的數學形式：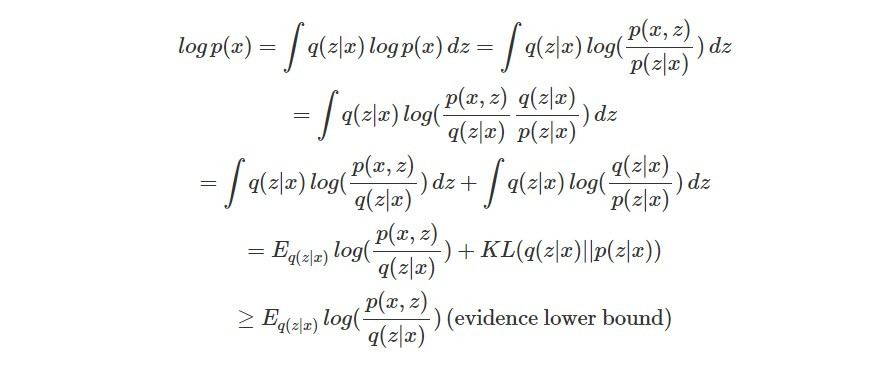

而 diffusion model 是由一連串的 denoise modules 組合起來的，我們可以這樣定義它的生成影像分布：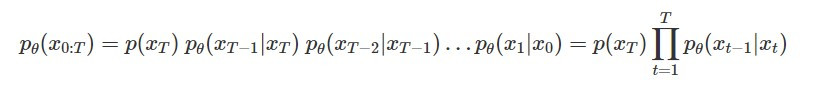

而它的 likelihood 的 lower bound，從 VAE 類推，則會是如下的形式：